Tambola

Tambola Quiz Game 🎲 (4x4 Grid) - Called Out Answers Highlight Only

Admin Panel - Manage Questions & Answers

Upload Excel file with columns: Question and Answer

Host Panel

Click "Next Question" to start

All Answers

(No answers to show yet)

Called Out Questions & Answers:

Generate Tambola Tickets

Grid size (N x N, max 10):
Number of tickets to generate (max 500):

Find All Triplets with Zero Sum

 

Problem Explanation: Find All Triplets with Zero Sum

The task is to find all unique triplets in an array that add up to zero. A triplet consists of three numbers, and the sum of these three numbers should be zero. For example:

Input: [-1, 0, 1, 2, -1, -4]
Output: [[-1, -1, 2], [-1, 0, 1]]

Approach to Solve the Problem

1. Sort the Array:
   First, sort the array in ascending order. Sorting helps to efficiently find the triplets using two pointers.

2. Fix One Element:
   Iterate through the array and fix one element. For each fixed element, find two other elements (using two pointers) such that their sum equals the negative of the fixed element.

3. Use Two Pointers:
   After fixing one element, use two pointers:

   • One pointer starts just after the fixed element.
   • The other pointer starts at the end of the array.
   • Move the pointers closer based on whether the current sum is less than, equal to, or greater than zero.

4. Avoid Duplicates:
   Skip duplicate elements to ensure the triplets are unique.

5. Add Valid Triplets:
   If the sum of the triplet is zero, add it to the result list.

---

Solution Code in Java

import java.util.*;

public class ZeroSumTriplets {

    public static List<List<Integer>> findTriplets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums); // Step 1: Sort the array

        for (int i = 0; i < nums.length - 2; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue; // Skip duplicates for the first element
            }

            int left = i + 1; // Pointer 1
            int right = nums.length - 1; // Pointer 2

            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];

                if (sum == 0) {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));

                    // Move both pointers and skip duplicates
                    while (left < right && nums[left] == nums[left + 1]) left++;
                    while (left < right && nums[right] == nums[right - 1]) right--;

                    left++;
                    right--;
                } else if (sum < 0) {
                    left++; // Move the left pointer to increase the sum
                } else {
                    right--; // Move the right pointer to decrease the sum
                }
            }
        }

        return result;
    }

    public static void main(String[] args) {
        int[] nums = {-1, 0, 1, 2, -1, -4};
        List<List<Integer>> triplets = findTriplets(nums);

        System.out.println("Triplets with zero sum: " + triplets);
    }
}

---

Explanation of the Code

1. Sorting: The array is sorted to simplify the two-pointer approach.
2. Outer Loop: Iterates through the array and fixes one element at a time.
3. Inner Logic with Two Pointers:
   • Adjusts pointers based on the sum of the triplet.
   • Adds valid triplets to the result list while skipping duplicates.
4. Output: The program prints all unique triplets with a zero sum.

---

Complexity

• Time Complexity:
  Sorting the array takes $O(n \log n)$, and the two-pointer approach runs in $O(n^2)$, making the overall complexity $O(n^2)$.
• Space Complexity:
  $O(n)$ for storing the result list.

This solution is efficient and easy to implement for finding triplets with zero sum.

UGC-NET COMPUTER SCIENCE PAPER-2 DECEMBER 2004

In this Blog we are providing all the UGC-NET Computer Science previous year Questions with explanation:

Q:: 1    A U A = A is called:

(A) Identity law             (B) De Morgan’s law

(C) Idempotent law       (D) Complement law

Answer: C

Explanation:

           (a) Commutative Laws:

                   For any two finite sets A and B;

                   (i) A U B = B U A

                   (ii) A ∩ B = B ∩ A

                   (b) Associative Laws:

                   For any three finite sets A, B and C;

                   (i) (A U B) U C = A U (B U C)

                   (ii) (A ∩ B) ∩ C = A ∩ (B ∩ C)

                   Thus, union and intersection are associative.

                   (c) Idempotent Laws:

                    For any finite set A;

                    (i) A U A = A

                    (ii) A ∩ A = A

                    (d) Distributive Laws:

                    For any three finite sets A, B and C;

                    (i) A U (B ∩ C) = (A U B) ∩ (A U C)

                    (ii) A ∩ (B U C) = (A ∩ B) U (A ∩ C)

                    Thus, union and intersection are distributive over intersection and union respectively.

                    (e) De Morgan’s Laws:

                    For any two finite sets A and B;

                    (i) A – (B U C) = (A – B) ∩ (A – C)

                    (ii) A - (B ∩ C) = (A – B) U (A – C)

                    De Morgan’s Laws can also we written as:

                    (i) (A U B)’ = A' ∩ B'

                    (ii) (A ∩ B)’ = A' U B'

                    (f) For any two finite sets A and B;

                    (i) A – B = A ∩ B'

                    (ii) B – A = B ∩ A'

                    (iii) A – B = A ⇔ A ∩ B = ∅

                    (iv) (A – B) U B = A U B

                    (v) (A – B) ∩ B = ∅

                    (vi) A ⊆ B ⇔ B' ⊆ A'

                    (vii) (A – B) U (B – A) = (A U B) – (A ∩ B)

                    (g) For any three finite sets A, B and C;

                    (i) A – (B ∩ C) = (A – B) U (A – C)

                    (ii) A – (B U C) = (A – B) ∩ (A – C)

                    (iii) A ∩ (B - C) = (A ∩ B) - (A ∩ C)

                    (iv) A ∩ (B △ C) = (A ∩ B) △ (A ∩ C)



Q:: 2  If f(x) =x+1 and g(x)=x+3 then fofofof is:

(A) g       (B) g+1

(C) g⁴     (D) None of the above

        Answer: B

Explanation:

            fofofof is f(f(f(x+1))) i.e. f(f(x+2)) i.e. f(x+3) similarly it is equal to "x+4".

            straight away it is clear that it is g(x)+1 i.e. (x+3)+1 = x+4.
            it could also be like : fog(x)=x+4 and gof(x)=x+4.

Q:: 3  The context-free languages are closed for:

(i) Intersection                          (ii) Union

(iii) Complementation              (iv) Kleene Star

then

(A) (i) and (iv)               (B) (i) and (iii)

(C) (ii) and (iv)              (D) (ii) and (iii)

Answer: C

Explanation:

             Closure properties of languages::

                      This entry lists some common closure properties on the families of languages corresponding to the Chomsky hierarchy, as well as other related families.

operation	REG	DCFL	CFL	CSL	RC	RE
union	Y	N	Y	Y	Y	Y
intersection	Y	N	N	Y	Y	Y
set difference	Y	N	N	Y	Y	N
complementation	Y	Y	N	Y	Y	N
intersection with a regular language	Y	Y	Y	Y	Y	Y
concatenation	Y	N	Y	Y	Y	Y
Kleene star	Y	N	Y	Y	Y	Y
Kleene plus	Y	N	Y	Y	Y	Y
reversal	Y	Y	Y	Y	Y	Y
lambda-free homomorphism	Y	N	Y	Y	Y	Y
homomorphism	Y	N	Y	N	N	Y
inverse homomorphism	Y	Y	Y	Y	Y	Y
lambda-free substitution	Y	N	Y	Y	Y	Y
substitution	Y	N	Y	N	N	Y
lambda-free GSM mapping	Y	N	Y	Y	Y	Y
GSM mapping	Y	N	Y	N	N	Y
inverse GSM mapping	Y	Y	Y	Y	Y	Y
lambda- limited erasing	Y		Y	Y		Y
rational transduction	Y	N	Y	N	N	Y
right quotient with a regular language	Y	Y	Y	N		Y
left quotient with a regular language	Y	Y	Y	N		Y

                 
                where the definitions of the cells in the top row are the following language families:

Abbreviation	Name
REG	regular
DCFL	deterministic context-free
CFL	context-free
CSL	context-sensitive
RC	recursive
RE	recursively enumerable

Q:: 4  Which of the following lists are the degrees of all the vertices of a graph:

(i) 1, 2, 3, 4, 5                (ii) 3, 4, 5, 6, 7

(iii) 1, 4, 5, 8, 6              (iv) 3, 4, 5, 6

then

(A) (i) and (ii)   

(B) (iii) and (iv)

(C) (iii) and (ii) 

(D) (ii) and (iv)

Answer: B

Explanation::
           Sum of degrees of the vertices of a graph should be even, So, only option (iii) and (iv) satisfy this.
           Sum of degrees of the vertices of a graph is equal to twice the number of edges.

Q:: 5   If I_m denotes the set of integers modulo m, then the following are fields with respect to the operations of addition modulo m and multiplication modulo m:

         (i) Z₂₃                    (ii) Z₂₉

         (iii) Z₃₁                  (iv) Z₃₃

         Then

         (A) (i) only                                

         (B) (i) and (ii) only

         (C) (i), (ii) and (iii) only           

         (D) (i), (ii), (iii) and (iv)

         Answer: C

Q:: 6    An example of a binary number which is equal to its 2’s complement is:

(A) 1100                        (B) 1001

(C) 1000                        (D) 1111

Answer: C

Explanation:

2's complement of (A) 1100 is 0100
2's complement of (B) 1001 is 0111
2's complement of (C) 1000 is 1000
2's complement of (D) 1111 is 0001

To calculate 2's complement of a binary number start from right side and copy down all 0's and

the first encountered 1, after that complement all subsequent bits 0 to 1 and 1 to 0.

Q:: 7   When a tri-state logic device is in the third state, then:
         (A) it draws low current 
         (B) it does not draw any current
         (C) it draws very high current
         (D) it presents a low impedance

Answer: D

Explanation:

In digital electronics three-state, tri-state, or 3-state logic allows an output port to assume a high impedance state in addition to the 0 and 1 logic levels, effectively removing the output from the circuit.
This allows multiple circuits to share the same output line or lines (such as a bus which cannot listen to more than one device at a time).Three-state outputs are implemented in many registers, bus drivers, and flip-flops in the 7400 and 4000 series as well as in other types, but also internally in many integrated circuits. Other typical uses are internal and external buses in microprocessors, computer memory, and peripherals. Many devices are controlled by an active-low input called OE(Output Enable) which dictates whether the outputs should be held in a high-impedance state or drive their respective loads (to either 0- or 1-level).

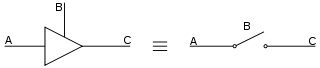A tri-state buffer can be thought of as a switch. If B is on, the switch is closed. If B is off, the switch is open.         

INPUT		OUTPUT
A	B	C
0	1	0
1		1
X	0	Z (high impedance)

Q:: 8   An example of a connective which is not associative is:

(A) AND             (B) OR

(C) EX-OR         (D) NAND

Answer: D

Explanation:
This can be proved by truth table::

            
As can be seen by inspection, the truth values under the main connectives do not match for all boolean interpretations.

Q:: 9    Essential hazards may occur in:

(A) Combinational logic circuits

(B) Synchronous sequential logic circuits

(C) Asynchronous sequential logic circuits working in the fundamental mode

(D) Asynchronous sequential logic circuits working in the pulse mode

Answer: C

Q::10.    The characteristic equation of a T flip-flop is:

   (A) Q_n+1=TQ’_n + T’ Q_n              

   (B) Q_n+1=T+Q_n

   (C) Q_n+1=TQ_n                            

   (D) Q_n+1= T’Q’_n

   The symbols used have the usual meaning.

Answer: A

Explanation:

FLIP-FLOP NAME	FLIP-FLOP SYMBOL	CHARACTERISTIC TABLE	CHARACTERISTIC EQUATION	EXCITATION TABLE
SR		S R Q(next) 0 0 Q 0 1 0 1 0 1 1 1 ?	Q(next) = S + R'QSR = 0	Q Q(next) S R 0 0 0 X 0 1 1 0 1 0 0 1 1 1 X 0
JK		J K Q(next) 0 0 Q 0 1 0 1 0 1 1 1 Q'	Q(next) = JQ' + K'Q	Q Q(next) J K 0 0 0 X 0 1 1 X 1 0 X 1 1 1 X 0
D		D Q(next) 0 0 1 1	Q(next) = D	Q Q(next) D 0 0 0 0 1 1 1 0 0 1 1 1
T		T Q(next) 0 Q 1 Q'	Q(next) = TQ' + T'Q	Q Q(next) T 0 0 0 0 1 1 1 0 1 1 1 0

Q::11.       Suppose x and y are two Integer Variables having values 0x5AB6 and 0x61CD respectively. The         result  (in hex) of applying bitwise operator AND to x and y will be:

    (A) 0x5089        (B) 0x4084

    (C) 0x78A4       (D) 0x3AD1

Answer: B

Explanation:

                 0x5AB6 = 0101 1010 1011 0110

                 0x61CD = 0110 0001 1100 1101

                 ----------------------------------------------

                 AND     =  0100 0000 1000 0100

                            =  0x4084

Q::12.   Consider the following statements,

   int i=4, j=3, k=0;

   k=++i - --j + i++ - --j +j++; What will be the values of i, j and k after the statement.

   (A) 7, 2, 8           (B) 5, 2, 10

   (C) 6, 2, 8           (D) 4, 2, 8

Answer: C

Explanation:

                The expression will be evaluated as k=5 - 2 + 5 - 1 + 1 => k=8.
                 i=6 and j=2.

Q::13.     What is the value of the arithmetic expression (Written in C)

   2*3/4-3/4* 2

   (A) 0                           (B) 1

   (C) 1.5                        (D) None of the above

Answer: B

Explanation:

          The expression will be evaluated as

           =>2*3/4-3/4* 2

           =>6/4-3/4* 2

           =>1-3/4* 2

           =>1-0*2

           =>1-0

           =>1.

Q::14  A function object:

(A) is an instance of a class for which operator () is a member function.

(B) is an instance of a class for which operator → is a member function.

(C) is a pointer to any function

(D) is a member function of a class

Answer: A

Explanation:

A function object, or functor, is any type that implements operator(). This operator is referred to as the call operator or sometimes the application operator. The Standard Template Library uses function objects primarily as sorting criteria for containers and in algorithms.

Function objects provide two main advantages over a straight function call. The first is that a function object can contain state. The second is that a function object is a type and therefore can be used as a template parameter.

To create a function object, create a type and implement operator(), such as:

 class Functor

    {
              public:
                 int operator()(int a, int b)
                 {
                       return a < b;
                 }
         };

         int main()
         {
              Functor f;
              int a = 5;
              int b = 7;
              int ans = f(a, b);
         }

The last line of the main function shows how you call the function object. This call looks like a call to a function, but it is actually calling operator() of the Functor type. This similarity between calling a function object and a function is how the term function object came about.





Q::15. Polymorphism means:

(A) A template function

(B) Runtime type identification within a class hierarchy

(C) Another name for operator overloading

(D) Virtual inheritance

Answer: B

Explanation:

                 In programming languages and type theory, polymorphism (from Greek πολύς, polys, "many, much" and μορφή, morphē, "form, shape") is the provision of a single interface to entities of different types. A polymorphic type is one whose operations can also be applied to values of some other type, or types. There are several fundamentally different kinds of Polymorphism:


Ad hoc polymorphism: When a function denotes different and potentially heterogeneous implementations depending on a limited range of individually specified types and combinations. Ad hoc polymorphism is supported in many languages using function overloading.


Parametric polymorphism: When code is written without mention of any specific type and thus can be used transparently with any number of new types. In the object-oriented programming community, this is often known as generics or generic programming. In the functional programming community, this is often shortened to polymorphism.


Subtyping (also called subtype polymorphism or inclusion polymorphism): When a name denotes instances of many different classes related by some common superclass. In the object-oriented programming community, this is often simply referred to as polymorphism.


The interaction between parametric polymorphism and subtyping leads to the concepts of variance and bounded quantification.

Q::16. The E-R model is expressed in terms of:

(i) Entities

(ii) The relationship among entities

(iii) The attributes of the entities

Then

(A) (i) and (iii)
(B) (i), (ii) and (iii)
(C) (ii) and (iii)
(D) None of the above

Answer: B

Explanation:
              The entity-relationship (E-R) data model perceives the real world as consisting of basic objects, called entities, and relationships among these objects. It was developed to facilitate database design by allowing specification of an enterprise schema, which represents the overall logical structure of a database. The E-R data model is one of several semantic data models; the semantic aspect of the model lies in its representation of the meaning of the data. The E-R model is very useful in mapping the meanings and interactions of real-world enterprises onto a conceptual schema. Because of this usefulness, many database-design tools draw on concepts from the E-R model.

Q::17. Specialization is a ............... process.

(A) Top - down (B) Bottom -Up

(C) Both (A) and (B) (D) None of the above

Answer: A

Explanation:

The process of designating subgroupings within an entity set is called specialization.An entity set may include subgroupings of entities that are distinct in some way from other entities in the set. For instance, a subset of entities within an entity set may have attributes that are not shared by all the entities in the entity set. The E-R model provides a means for representing these distinctive entity groupings. Consider an entity set person, with attributes name, street, and city. 

A person may be further classified as one of the following:

• customer

• employee

Each of these person types is described by a set of attributes that includes all the attributes of entity set person plus possibly additional attributes. For example, customer entities may be described further by the attribute customer-id, whereas employee entities may be described further by the attributes employee-id and salary.The specialization of person allows us to distinguish among persons according to whether they are employees or customers.

Q::18.    The completeness constraint has rules:

   (A) Supertype, Subtype

   (B) Total specialization, Partial specialization

   (C) Specialization, Generalization

   (D) All of the above

Answer: B

Explanation:

The completeness constraint on a generalization or specialization, specifies whether or not an entity in the higher-level entity set must belong to at least one of the lower-level entity sets within the generalization/specialization. This constraint may be one of the following:



• Total generalization or specialization:Each higher-level entity must belong to a lower-level entity set.

• Partial generalization or specialization: Some higher-level entities may not belong to any lower-level entity set.

Partial generalization is the default.We can specify total generalization in an E-R diagram by using a double line to connect the box representing the higher-level entity set to the triangle symbol.

We can see that certain insertion and deletion requirements follow from the constraints that apply to a given generalization or specialization. For instance, when a total completeness constraint is in place, an entity inserted into a higher-level entity set must also be inserted into at least one of the lower-level entity sets. With a condition-defined constraint, all higher-level entities that satisfy the condition must be inserted into that lower-level entity set. Finally, an entity that is deleted from a higher-level entity set also is deleted from all the associated lower-level entity sets to which it belongs.

Q::19.   The entity type on which the ................. type depends is called the identifying owner.

   (A) Strong entity                  (B) Relationship

   (C) Weak entity                     (D) E - R

Answer: C







Explanation:

An entity set may not have sufficient attributes to form a primary key. Such an entity set is termed a weak entity set. An entity set that has a primary key is termed a strong entity set. As an illustration, consider the entity set payment, which has the three attributes: {payment-number, payment-date, payment-amount}. Payment numbers are typically sequential numbers, starting from 1, generated separately for each loan. Thus, although each payment entity is distinct, payments for different loans may share the same payment number. Thus, this entity set does not have a primary key; it is a weak
entity set. For a weak entity set to be meaningful, it must be associated with another entity set, called the identifying or owner entity set. Every weak entity must be associated with an identifying entity; that is, the weak entity set is said to be existence dependent on the identifying entity set. The identifying entity set is said to own the weak entity set that it identifies. The relationship associating the weak entity set with the identifying entity set is called the identifying relationship. The identifying relationship is many to one from the weak entity set to the identifying entity set, and the participation of the weak entity set in the relationship is total. In our example, the identifying entity set for payment is loan, and a relationship loan-payment that associates payment entities with their corresponding loan entities is the identifying relationship. Although a weak entity set does not have a primary key, we nevertheless need a means of distinguishing among all those entities in the weak entity set that depend on one particular strong entity. The discriminator of a weak entity set is a set of attributes that allows this distinction to be made. For example, the discriminator of the weak entity set payment is the attribute payment-number, since, for each loan, a payment number uniquely identifies one single payment for that loan. The discriminator of a weak entity set is also called the partial key of the entity set. The primary key of a weak entity set is formed by the primary key of the identifying entity set, plus the weak entity set’s discriminator. In the case of the entity set payment, its primary key is {loan-number, payment-number}, where loan-number is the primary key of the identifying entity set, namely loan, and payment-number distinguishes payment entities within the same loan.

Q::20.    Match the following:

(i) 5 NF              (a) Transitive dependencies eliminated

(ii) 2 NF             (b) Multivalued attribute removed

(iii) 3 NF             (c) Contains no partial functional dependencies

(iv) 4 NF             (d) Contains no join dependency

(A) i-a, ii-c, iii-b, iv-d    

(B) i-d, ii-c, iii-a, iv-b

(C) i-d, ii-c, iii-b, iv-a   

(D) i-a, ii-b, iii-c, iv-d

Answer: B

Explanation:

First Normal Form

The first of the normal forms that we study, first normal form, imposes a very basic requirement on relations; unlike the other normal forms, it does not require additional information such as functional dependencies. A domain is atomic if elements of the domain are considered to be indivisible units. We say that a relation schema R is in first normal form (1NF) if the domains of all attributes of R are atomic. A set of names is an example of a nonatomic value. For example, if the schema of a relation employee included an attribute children whose domain elements are sets of names, the schema would not be in first normal form. Composite attributes, such as an attribute address with component attributes street and city, also have non-atomic domains.

Second Normal Form

A table that is in first normal form (1NF) must meet additional criteria if it is to qualify for second normal form. Specifically: a table is in 2NF if it is in 1NF and no non-prime attribute is dependent on any proper subset of any candidate key of the table. A non-prime attribute of a table is an attribute that is not a part of any candidate key of the table.A functional dependency on part of any candidate key is a violation of 2NF. In addition to the primary key, the table may contain other candidate keys; it is necessary to establish that no non-prime attributes have part-key dependencies on any of these candidate keys.

Q::21.       What item is at the root after the following sequence of insertions into an empty splay tree:

1, 11, 3, 10, 8, 4, 6, 5, 7, 9, 2 ?

(A) 1       (B) 2

(C) 4       (D) 8

Answer: B

Explanation:

A splay tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O(log n) amortized time(amortized analysis is a method for analyzing a given algorithm's time complexity). For many sequences of non-random operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown. The splay tree was invented by Daniel Dominic Sleator and Robert Endre Tarjan in 1985.

All normal operations on a binary search tree are combined with one basic operation, called splaying. Splaying the tree for a certain element rearranges the tree so that the element is placed at the root of the tree. One way to do this is to first perform a standard binary tree search for the element in question, and then use tree rotations in a specific fashion to bring the element to the top. Alternatively, a top-down algorithm can combine the search and the tree reorganization into a single phase.

For more details visit 

http://cbsenetmaterial.blogspot.in/2015/11/ugc-net-computer-science-splay-tree.html

Q::22.       Suppose we are implementing quadratic probing with a Hash function, Hash (y)=X mode 100. If an element with key 4594 is inserted and the first three locations attempted are already occupied, then the next cell that will be tried is:

(A) 2       (B) 3

(C) 9       (D) 97

Answer: B

Explanation:

h(4594) = 94 i.e. our first attempt

94 + 1^2 = 95 second attempt

94 + 2^2 = 98 third attempt

94 + 3^2 = 103 % 100 = 3 i.e. next cell to be tried will be 3.

Q::23. Weighted graph:

(A) Is a bi-directional graph

(B) Is directed graph

(C) Is graph in which number associated with arc

(D) Eliminates table method

Answer: C

Explanation:
A weight is a numerical value, assigned as a label to a vertex or edge of a graph. A weighted graph is a graph whose vertices or edges have been assigned weights; more specifically, a vertex-weighted graph has weights on its vertices and an edge-weighted graph has weights on its edges. The weight of a subgraph is the sum of the weights of the vertices or edges within that subgraph.

Q::24. What operation is supported in constant time by the doubly linked list, but not by the singly linked list?

(A) Advance     (B) Backup

(C) First            (D) Retrieve

Answer: B

Q::25.       How much extra space is used by heap sort?

(A) O(1)              (B) O(Log n)

(C) O(n)             (D) O(n²)

Answer: A

Explanation:

A run of the heapsort algorithm sorting an array of randomly permuted values. In the first stage of the algorithm the array elements are reordered to satisfy the heap property. Before the actual sorting takes place, the heap tree structure is shown briefly for illustration.
Class	Sorting algorithm
Data structure	Array
Worst case performance
Best case performance	[1]
Average case performance
Worst case space complexity	auxiliary

Q::26.Error control is needed at the transport layer because of potential error occurring ..............

(A) from transmission line noise

(B) in router

(C) from out of sequence delivery

(D) from packet losses

Answer:

Explanation:TCP is a reliable transport layer protocol. This means that an application program that delivers a stream of data to TCP relies on TCP to deliver the entire stream to the application program on the other end in order, without error, and without any part lost or duplicated. TCP provides reliability using error control. Error control includes mechanisms for detecting corrupted segments, lost segments, out-of-order segments, and duplicated segments. Error control also includes a mechanism for correcting errors after they are detected. Error detection and correction in TCP is achieved through the use of three simple tools: checksum, acknowledgment, and time-out.

Q::27. Making sure that all the data packets of a message are delivered to the destination is ................ control.

(A) Error (B) Loss

(C) Sequence (D) Duplication

Answer: A

Q::28.       Which transport class should be used with a perfect network layer?

(A) TP0 and TP2          (B) TP1 and TP3

(C) TP0, TP1, TP3       (D) TP0, TP1, TP2, TP3, TP4
Answer: A

Q::29. Which transport class should be used with residual-error network layer? 

(A) TP0, TP2 (B) TP1, TP3 

(C) TP1, TP3, TP4 (D) TP0, TP1, TP2, TP3, TP4 

Answer: B 

Q::30. Virtual circuit is associated with a ..................... service.


(A) Connectionless (B) Error-free


(C) Segmentation (D) Connection-oriented

Answer: D

Explanation:

A virtual-circuit network is a cross between a circuit-switched network and a datagram network. It has some characteristics of both.

(a)As in a circuit-switched network, there are setup and teardown phases in addition to the data transfer phase.

(b) Resources can be allocated during the setup phase, as in a circuit-switched network,

or on demand, as in a datagram network. 

(c) As in a datagram network, data are packetized and each packet carries an address in

the header. However, the address in the header has local jurisdiction (it defines what

should be the next switch and the channel on which the packet is being canied), not

end-to-end jurisdiction.

(d) As in a circuit-switched network, all packets follow the same path established during

the connection.

(e) A virtual-circuit network is normally implemented in the data link layer, while a

circuit-switched network is implemented in the physical layer and a datagram network

in the network layer. But this may change in the future.

Q::31. Which activity is not included in the first pass of two pass assemblers?

(A) Build the symbol table

(B) Construct the intermediate code

(C) Separate mnemonic opcode and operand fields

(D) None of the above

Answer: D

Explanation:

An assembler is a translator, that translates an assembler program into a conventional machine language program. Basically, the assembler goes through the program one line at a time, and generates machine code for that instruction. Then the assembler procedes to the next instruction. In this way, the entire machine code program is created. For most instructions this process works fine, for example for instructions that only reference registers, the assembler can compute the machine code easily, since the assembler knows where the registers are.

Consider an assembler instruction like the following

          JMP  LATER
          ...
          ...
LATER:

This is known as a forward reference. If the assembler is processing the file one line at a time, then it doesn't know where LATER is when it first encounters the jump instruction. So, it doesn't know if the jump is a short jump, a near jump or a far jump. There is a large difference amongst these instructions. They are 2, 3, and 5 bytes long respectively. The assembler would have to guess how far away the instruction is in order to generate the correct instruction. If the assembler guesses wrong, then the addresses for all other labels later in the program woulds be wrong, and the code would have to be regenerated. Or, the assembler could alway choose the worst case. But this would mean generating inefficiency in the program, since all jumps would be considered far jumps and would be 5 bytes long, where actually most jumps are short jumps, which are only 2 bytes long.

Soooooooo, what is to be done to allow the assembler to generate the correct instruction? Answer: scan the code twice. The first time, just count how long the machine code instructions will be, just to find out the addresses of all the labels. Also, create a table that has a list of all the addresses and where they will be in the program. This table is known as the symbol table. On the second scan, generate the machine code, and use the symbol table to determine how far away jump labels are, and to generate the most efficient instruction.

This is known as a two-pass assembler. Each pass scans the program, the first pass generates the symbol table and the second pass generates the machine code.

First Pass

On the first pass, the assembler performs the following tasks:

• Checks to see if the instructions are legal in the current assembly mode.
• Allocates space for instructions and storage areas you request.
• Fills in the values of constants, where possible.
• Builds a symbol table, also called a cross-reference table, and makes an entry in this table for every symbol it encounters in the label field of a statement.

The assembler reads one line of the source file at a time. If this source statement has a valid symbol in the label field, the assembler ensures that the symbol has not already been used as a label. If this is the first time the symbol has been used as a label, the assembler adds the label to the symbol table and assigns the value of the current location counter to the symbol. If the symbol has already been used as a label, the assembler returns the error message Redefinition of symbol and reassigns the symbol value.

Next, the assembler examines the instruction's mnemonic. If the mnemonic is for a machine instruction that is legal for the current assembly mode, the assembler determines the format of the instruction (for example, XO format). The assembler then allocates the number of bytes necessary to hold the machine code for the instruction. The contents of the location counter are incremented by this number of bytes.

When the assembler encounters a comment (preceded by a # (pound sign)) or an end-of-line character, the assembler starts scanning the next instruction statement. The assembler keeps scanning statements and building its symbol table until there are no more statements to read.

At the end of the first pass, all the necessary space has been allocated and each symbol defined in the program has been associated with a location counter value in the symbol table. When there are no more source statements to read, the second pass starts at the beginning of the program.

Note: If an error is found in the first pass, the assembly process terminates and does not continue to the second pass. If this occurs, the assembler listing only contains errors and warnings generated during the first pass of the assembler.

Second Pass

On the second pass, the assembler:

• Examines the operands for symbolic references to storage locations and resolves these symbolic references using information in the symbol table.
• Ensures that no instructions contain an invalid instruction form.
• Translates source statements into machine code and constants, thus filling the allocated space with object code.
• Produces a file containing error messages, if any have occurred.

At the beginning of the second pass, the assembler scans each source statement a second time. As the assembler translates each instruction, it increments the value contained in the location counter.

If a particular symbol appears in the source code, but is not found in the symbol table, then the symbol was never defined. That is, the assembler did not encounter the symbol in the label field of any of the statements scanned during the first pass, or the symbol was never the subject of a .comm, .csect, .lcomm, .sect, or .set pseudo-op.

This could be either a deliberate external reference or a programmer error, such as misspelling a symbol name. The assembler indicates an error. All external references must appear in a .extern or .globl statement.

The assembler logs errors such as incorrect data alignment. However, many alignment problems are indicated by statements that do not halt assembly. The -w flag must be used to display these warning messages.

After the programmer corrects assembly errors, the program is ready to be linked.

Note:

If only warnings are generated in the first pass, the assembly process continues to the second pass. The assembler listing contains errors and warnings generated during the second pass of the assembler. Any warnings generated in the first pass do not appear in the assembler listing.

Q::32. Which of the following is not collision resolution technique?

(A) Hash addressing (B) Chaining

(C) Both (A) and (B) (D) Indexing

Answer: D

Explanation:

Open addressing, or closed hashing, is a method of collision resolution in hash tables. With this method a hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:

Linear probing  in which the interval between probes is fixed — often at 1.

Quadratic probing  in which the interval between probes increases linearly (hence, the indices are described by a quadratic function).

Double hashing in which the interval between probes is fixed for each record but is computed by another hash function.

Chaining

Hash collision resolved by separate chaining.

In the method known as separate chaining, each bucket is independent, and has some sort of list of entries with the same index. The time for hash table operations is the time to find the bucket (which is constant) plus the time for the list operation.
In a good hash table, each bucket has zero or one entries, and sometimes two or three, but rarely more than that. Therefore, structures that are efficient in time and space for these cases are preferred. Structures that are efficient for a fairly large number of entries per bucket are not needed or desirable. If these cases happen often, the hashing is not working well, and this needs to be fixed.

Indexing:
Indexing is a data structure technique to efficiently retrieve records from the database files based on some attributes on which the indexing has been done. Indexing in database systems is similar to what we see in books.
Indexing is defined based on its indexing attributes. Indexing can be of the following types −

Primary Index − Primary index is defined on an ordered data file. The data file is ordered on a key field. The key field is generally the primary key of the relation.


Secondary Index − Secondary index may be generated from a field which is a candidate key and has a unique value in every record, or a non-key with duplicate values.


Clustering Index − Clustering index is defined on an ordered data file. The data file is ordered on a non-key field.

Q::33. Code optimization is responsibility of: 

(A) Application programmer 

(B) System programmer 

(C) Operating system 

(D) All of the above 

Answer: B

Explanation:

Code optimization is any method of code modification to improve code quality and efficiency. A program may be optimized so that it becomes a smaller size, consumes less memory, executes more rapidly, or performs fewer input/output operations.

The basic requirements optimization methods should comply with, is that an optimized program must have the same output and side effects as its non-optimized version. This requirement, however, may be ignored in the case that the benefit from optimization, is estimated to be more important than probable consequences of a change in the program behavior.

In optimization, high-level general programming constructs are replaced by very efficient low-level programming codes. A code optimizing process must follow the three rules given below: 

The output code must not, in any way, change the meaning of the program. Optimization should increase the speed of the program and if possible, the program should demand less number of resources. 

Optimization should itself be fast and should not delay the overall compiling process.  Efforts for an optimized code can be made at various levels of compiling the process. At the beginning, users can change/rearrange the code or use better algorithms to write the code. After generating intermediate code, the compiler can modify the intermediate code by address calculations and improving loops. While producing the target machine code, the compiler can make use of memory hierarchy and CPU registers. 

Q::34 Which activity is included in the first pass of two pass assemblers?

(A) Build the symbol table

(B) Construct the intermediate code

(C) Separate mnemonic opcode and operand fields

(D) None of these

Answer: A,B,C

Explanation:

Refer to Question no. 31

Q::35.In two pass assembler the symbol table is used to store:

(A) Label and value    (B) Only value

(C) Mnemonic              (D) Memory Location

Answer: D

Refer to Question no. 31

Q::36.Semaphores are used to:

(A) Synchronise critical resources to prevent deadlock

(B) Synchronise critical resources to prevent contention

(C) Do I/o

(D) Facilitate memory management

Answer: 
Explanation:

A semaphore, in its most basic form, is a protected integer variable that can facilitate and restrict access to shared resources in a multi-processing environment. The two most common kinds of semaphores are counting semaphores and binary semaphores. Counting semaphores represent multiple resources, while binary semaphores, as the name implies, represents two possible states (generally 0 or 1; locked or unlocked). Semaphores were invented by the late Edsger Dijkstra.

Semaphores can be looked at as a representation of a limited number of resources, like seating capacity at a restaurant. If a restaurant has a capacity of 50 people and nobody is there, the semaphore would be initialized to 50. As each person arrives at the restaurant, they cause the seating capacity to decrease, so the semaphore in turn is decremented. When the maximum capacity is reached, the semaphore will be at zero, and nobody else will be able to enter the restaurant. Instead the hopeful restaurant goers must wait until someone is done with the resource, or in this analogy, done eating. When a patron leaves, the semaphore is incremented and the resource becomes available again.

A semaphore can only be accessed using the following operations: wait() and signal(). wait() is called when a process wants access to a resource. This would be equivalent to the arriving customer trying to get an open table. If there is an open table, or the semaphore is greater than zero, then he can take that resource and sit at the table. If there is no open table and the semaphore is zero, that process must wait until it becomes available. signal() is called when a process is done using a resource, or when the patron is finished with his meal. 

Q::37 In which of the following storage replacement strategies, is a program placed in the largest available hole in the memory?

(A) Best fit         (B) First fit

(C) Worst fit       (D) Buddy

Answer: C

Q::38 Remote computing system involves the use of timesharing systems and:

(A) Real time processing        (B) Batch processing

(C) Multiprocessing                 (D) All of the above

Answer: B

Q::39 Non modifiable procedures are called

(A) Serially useable procedures      

(B) Concurrent procedures

(C) Reentrant procedures                 

(D) Topdown procedures

Answer: C
Explanation:

In computing, a computer program or subroutine is called reentrant if it can be interrupted in the middle of its execution and then safely called again ("re-entered") before its previous invocations complete execution. The interruption could be caused by an internal action such as a jump or call, or by an external action such as a hardware interrupt or signal. Once the reentered invocation completes, the previous invocations will resume correct execution.

This definition originates from single-threaded programming environments where the flow of control could be interrupted by a hardware interrupt and transferred to an interrupt service routine (ISR). Any subroutine used by the ISR that could potentially have been executing when the interrupt was triggered should be reentrant. Often, subroutines accessible via the operating system kernel are not reentrant. Hence, interrupt service routines are limited in the actions they can perform; for instance, they are usually restricted from accessing the file system and sometimes even from allocating memory.

A subroutine that is directly or indirectly recursive should be reentrant. This policy is partially enforced by structured programming languages. However a subroutine can fail to be reentrant if it relies on a global variable to remain unchanged but that variable is modified when the subroutine is recursively invoked.
Reentrant code may not hold any static (or global) non-constant data.

Reentrant functions can work with global data. For example, a reentrant interrupt service routine could grab a piece of hardware status to work with (e.g. serial port read buffer) which is not only global, but volatile. Still, typical use of static variables and global data is not advised, in the sense that only atomic read-modify-write instructions should be used in these variables (it should not be possible for an interrupt or signal to come during the execution of such an instruction).

Reentrant code may not modify its own code.

The operating system might allow a process to modify its code. There are various reasons for this (e.g., blitting graphics quickly) but this would cause a problem with reentrancy, since the code might not be the same next time.

It may, however, modify itself if it resides in its own unique memory. That is, if each new invocation uses a different physical machine code location where a copy of the original code is made, it will not affect other invocations even if it modifies itself during execution of that particular invocation (thread).

Reentrant code may not call non-reentrant computer programs or routines.

Multiple levels of 'user/object/process priority' and/or multiprocessing usually complicate the control of reentrant code. It is important to keep track of any access and or side effects that are done inside a routine designed to be reentrant.

Q::40 Match the following

(a) Disk scheduling                 (1) Round robin

(b) Batch processing               (2) Scan

(c) Time sharing                       (3) LIFO

(d) Interrupt processing          (4) FIFO

(A) a-3, b-4, c-2, d-1    

(B) a-4, b-3, c-2, d-1

(C) a-2, b-4, c-1, d-3   

(D) a-3, b-4, c-1, d-2

Answer: C

Q::41 The main objective of designing various modules of a software system is:

(A) To decrease the cohesion and to increase the coupling

(B) To increase the cohesion and to decrease the coupling

(C) To increase the coupling only

(D) To increase the cohesion only

Answer: B

Explanation:

In computer programming, cohesion refers to the degree to which the elements of a module belong together. Thus, cohesion measures the strength of relationship between pieces of functionality within a given module. For example, in highly cohesive systems functionality is strongly related.

Cohesion is an ordinal type of measurement and is usually described as “high cohesion” or “low cohesion”. Modules with high cohesion tend to be preferable because high cohesion is associated with several desirable traits of software including robustness, reliability, reusability, and understandability whereas low cohesion is associated with undesirable traits such as being difficult to maintain, test, reuse, or even understand.

Cohesion is often contrasted with coupling, a different concept. High cohesion often correlates with loose coupling, and vice versa.

Cohesion is a qualitative measure, meaning that the source code to be measured is examined using a rubric to determine a classification. Cohesion types, from the worst to the best, are as follows:

Coincidental cohesion (worst)

Coincidental cohesion is when parts of a module are grouped arbitrarily; the only relationship between the parts is that they have been grouped together (e.g. a “Utilities” class).

Logical cohesion

Logical cohesion is when parts of a module are grouped because they are logically categorized to do the same thing even though they are different by nature (e.g. grouping all mouse and keyboard input handling routines).

Temporal cohesion

Temporal cohesion is when parts of a module are grouped by when they are processed - the parts are processed at a particular time in program execution (e.g. a function which is called after catching an exception which closes open files, creates an error log, and notifies the user).

Procedural cohesion

Procedural cohesion is when parts of a module are grouped because they always follow a certain sequence of execution (e.g. a function which checks file permissions and then opens the file).

Communicational/informational cohesion

Communicational cohesion is when parts of a module are grouped because they operate on the same data (e.g. a module which operates on the same record of information).

Sequential cohesion

Sequential cohesion is when parts of a module are grouped because the output from one part is the input to another part like an assembly line (e.g. a function which reads data from a file and processes the data).

Functional cohesion (best)

Functional cohesion is when parts of a module are grouped because they all contribute to a single well-defined task of the module (e.g. Lexical analysis of an XML string).

Coupling

In software engineering, coupling is the manner and degree of interdependence between software modules; a measure of how closely connected two routines or modules are; the strength of the relationships between modules.

Coupling is usually contrasted with cohesion. Low coupling often correlates with high cohesion, and vice versa. Low coupling is often a sign of a well-structured computer system and a good design, and when combined with high cohesion, supports the general goals of high readability and maintainability.

Content coupling (high)

Content coupling (also known as Pathological coupling) occurs when one module modifies or relies on the internal workings of another module (e.g., accessing local data of another module).

Therefore changing the way the second module produces data (location, type, timing) will lead to changing the dependent module.

Common coupling

Common coupling (also known as Global coupling) occurs when two modules share the same global data (e.g., a global variable).

Changing the shared resource implies changing all the modules using it.

External coupling

External coupling occurs when two modules share an externally imposed data format, communication protocol, or device interface. This is basically related to the communication to external tools and devices.

Control coupling

Control coupling is one module controlling the flow of another, by passing it information on what to do (e.g., passing a what-to-do flag).

Stamp coupling (Data-structured coupling)

Stamp coupling occurs when modules share a composite data structure and use only a part of it, possibly a different part (e.g., passing a whole record to a function that only needs one field of it).

This may lead to changing the way a module reads a record because a field that the module does not need has been modified.

Data coupling

Data coupling occurs when modules share data through, for example, parameters. Each datum is an elementary piece, and these are the only data shared (e.g., passing an integer to a function that computes a square root).

Message coupling (low)

This is the loosest type of coupling. It can be achieved by state decentralization (as in objects) and component communication is done via parameters or message passing (see Message passing).

No coupling

Modules do not communicate at all with one another.

Q::42 Three essential components of a software project plan are:

(A) Team structure, Quality assurance plans, Cost estimation

(B) Cost estimation, Time estimation, Quality assurance plan

(C) Cost estimation, Time estimation, Personnel estimation

(D) Cost estimation, Personnel estimation, Team structure

Answer: B

Q::43 Reliability of software is dependent on:

(A) Number of errors present in software

(B) Documentation

(C) Testing suties

(D) Development Processes

Answer: A

Explanation:

Ability of a computer program to perform its intended functions and operations in a system's environment, without experiencing failure (system crash).Software Reliability is the probability of failure-free software operation for a specified period of time in a specified environment. Software Reliability is also an important factor affecting system reliability. It differs from hardware reliability in that it reflects the design perfection, rather than manufacturing perfection. The high complexity of software is the major contributing factor of Software Reliability problems. Software Reliability is not a function of time - although researchers have come up with models relating the two.

Q::44 In transform analysis, input portion is called:

(A) Afferent branch                 (B) Efferent branch

(C) Central Transform             (D) None of the above

Answer: A

Explanation:

A structure chart is produced by the conversion of a DFD diagram; this conversion is described as ‘transform mapping (analysis)’. It is applied through the ‘transforming’ of input data flow into output data flow.

Transform analysis establishes the modules of the system, also known as the primary functional components, as well as the inputs and outputs of the identified modules in the DFD. Transform analysis is made up of a number of steps that need to be carried out. The first one is the dividing of the DFD into 3 parts:

Input

Logical processing

Output

The ‘input’ part of the DFD covers operations that change high level input data from physical to logical form e.g. from a keyboard input to storing the characters typed into a database. Each individual instance of an input s called an ‘afferent branch’.

The ‘output’ part of the DFD is similar to the ‘input’ part in that it acts as a conversion process. However, the conversion is concerned with the logical output of the system into a physical one e.g. text stored in a database converted into a printed version through a printer. Also, similar to the ‘input’, each individual instance of an output is called as ‘efferent branch’. The remaining part of a DFD is called the central transform.

Once the above step has been conducted, transform analysis moves onto the second step; the structure chart is established by identifying one module for the central transform, the afferent and efferent branches. These are controlled by a ‘root module’ which acts as an ‘invoking’ part of the DFD.

In order to establish the highest input and output conversions in the system, a ‘bubble’ is drawn out. In other words, the inputs are mapped out to their outputs until an output is found that cannot be traced back to its input. Central transforms can be classified as processes that manipulate the inputs/outputs of a system e.g. sorting input, prioritizing it or filtering data. Processes which check the inputs/outputs or attach additional information to them cannot be classified as central transforms. Inputs and outputs are represented as boxes in the first level structure chart and central transforms as single boxes.

Moving on to the third step of transform analysis, sub-functions (formed from the breaking up of high-level functional components, a process called ‘factoring’) are added to the structure chart. The factoring process adds sub-functions that deal with error-handling and sub-functions that determine the start and end of a process.

Transform analysis is a set of design steps that allows a DFD with transform flow characteristics to be mapped into specific architectural style. These steps are as follows:

Step1: Review the fundamental system model

Step2: Review and refine DFD for the SW

Step3: Assess the DFD in order to decide the usage of transform or transaction flow.

Step4: Identify incoming and outgoing boundaries in order to establish the transform center.

Step5: Perform "first-level factoring".

Step6: Perform "second-level factoring".

Step7: Refine the first-iteration architecture using design heuristics for improved SW quality.

Q::45 The Function Point (FP) metric is:

(A) Calculated from user requirements

(B) Calculated from Lines of code

(C) Calculated from software’s complexity assessment

(D) None of the above

Answer: C

Explanation:

Function point metric was proposed by Albrecht [1983]. This metric overcomes many of the shortcomings of the LOC metric. Since its inception in late 1970s, function point metric has been slowly gaining popularity. One of the important advantages of using the function point metric is that it can be used to easily estimate the size of a software product directly from the problem specification. This is in contrast to the LOC metric, where the size can be accurately determined only after the product has fully been developed. The conceptual idea behind the function point metric is that the size of a software product is directly dependent on the number of different functions or features it supports. A software product supporting many features would certainly be of larger size than a product with less number of features. Each function when invoked reads some input data and transforms it to the corresponding output data. For example, the issue book feature of a Library Automation Software takes the name of the book as input and displays its location and the number of copies available. Thus, a computation of the number of input and the output data values to a system gives some indication of the number of functions supported by the system. Albrecht postulated that in addition to the number of basic functions that a software performs, the size is also dependent on the number of files and the number of interfaces.

Besides using the number of input and output data values, function point metric computes the size of a software product (in units of functions points or FPs) using three other characteristics of the product as shown in the following expression. The size of a product in function points (FP) can be expressed as the weighted sum of these five problem characteristics. The weights associated with the five characteristics were proposed empirically and validated by the observations over many projects. Function point is computed in two steps. The first step is to compute the unadjusted function point (UFP).

UFP = (Number of inputs)*4 + (Number of outputs)*5 + (Number of inquiries)*4 +

(Number of files)*10 + (Number of interfaces)*10

Number of inputs: Each data item input by the user is counted. Data inputs should be distinguished from user inquiries. Inquiries are user commands such as print-account-balance. Inquiries are counted separately. It must be noted that individual data items input by the user are not considered in the calculation of the number of inputs, but a group of related inputs are considered as a single input.
For example, while entering the data concerning an employee to an employee pay roll software; the data items name, age, sex, address, phone number, etc. are together considered as a single input. All these data items can be considered to be related, since they pertain to a single employee.

Number of outputs: The outputs considered refer to reports printed, screen outputs, error messages produced, etc. While outputting the number of outputs the individual data items within a report are not considered, but a set of related data items is counted as one input.

Number of inquiries: Number of inquiries is the number of distinct interactive queries which can be made by the users. These inquiries are the user commands which require specific action by the system.

Number of files: Each logical file is counted. A logical file means groups of logically related data. Thus, logical files can be data structures or physical files.

Number of interfaces: Here the interfaces considered are the interfaces used to exchange information with other systems. Examples of such interfaces are data files on tapes, disks, communication links with other systems etc.

Once the unadjusted function point (UFP) is computed, the technical complexity factor (TCF) is computed next. TCF refines the UFP measure by considering fourteen other factors such as high transaction rates, throughput, and response time requirements, etc. Each of these 14 factors is assigned from 0 (not present or no influence) to 6 (strong influence). The resulting numbers are summed, yielding the total degree of influence (DI). Now, TCF is computed as

(0.65+0.01*DI). As DI can vary from 0 to 70, TCF can vary from 0.65 to 1.35.
Finally, FP=UFP*TCF.

Q::46.       Data Mining can be used as ................. Tool.

(A) Software     (B) Hardware

(C) Research    (D) Process

Answer: C

Explanation:

Data mining is an interdisciplinary subfield of computer science. It is the computational process of discovering patterns in large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics, and database systems. The overall goal of the data mining process is to extract information from a data set and transform it into an understandable structure for further use. Aside from the raw analysis step, it involves database and data management aspects, data pre-processing, model and inference considerations, interestingness metrics, complexity considerations, post-processing of discovered structures, visualization, and online updating. Data mining is the analysis step of the "knowledge discovery in databases" process, or KDD.

The term is a misnomer, because the goal is the extraction of patterns and knowledge from large amounts of data, not the extraction (mining) of data itself. It also is a buzzword and is frequently applied to any form of large-scale data or information processing (collection, extraction, warehousing, analysis, and statistics) as well as any application of computer decision support system, including artificial intelligence, machine learning, and business intelligence.

The actual data mining task is the automatic or semi-automatic analysis of large quantities of data to extract previously unknown, interesting patterns such as groups of data records (cluster analysis), unusual records (anomaly detection), and dependencies (association rule mining). This usually involves using database techniques such as spatial indices. These patterns can then be seen as a kind of summary of the input data, and may be used in further analysis or, for example, in machine learning and predictive analytics. For example, the data mining step might identify multiple groups in the data, which can then be used to obtain more accurate prediction results by a decision support system. Neither the data collection, data preparation, nor result interpretation and reporting is part of the data mining step, but do belong to the overall KDD process as additional steps.


The related terms data dredging, data fishing, and data snooping refer to the use of data mining methods to sample parts of a larger population data set that are (or may be) too small for reliable statistical inferences to be made about the validity of any patterns discovered. These methods can, however, be used in creating new hypotheses to test against the larger data populations.

Q::47 The processing speeds of pipeline segments are usually:

(A) Equal           (B) Unequal

(C) Greater        (D) None of these

Answer: B

Explanation:

Pipelining

In computing, a pipeline is a set of data processing elements connected in series, where the output of one element is the input of the next one. The elements of a pipeline are often executed in parallel or in time-sliced fashion; in that case, some amount of buffer storage is often inserted between elements.

Computer-related pipelines include:

Instruction pipelines, such as the classic RISC pipeline, which are used in central processing units (CPUs) to allow overlapping execution of multiple instructions with the same circuitry. The circuitry is usually divided up into stages, including instruction decoding, arithmetic, and register fetching stages, wherein each stage processes one instruction at a time.
Graphics pipelines, found in most graphics processing units (GPUs), which consist of multiple arithmetic units, or complete CPUs, that implement the various stages of common rendering operations (perspective projection, window clipping, color and light calculation, rendering, etc.).

Software pipelines, where commands can be written where the output of one operation is automatically fed to the next, following operation. The Unix system call pipe is a classic example of this concept, although other operating systems do support pipes as well.
Example: Pipelining is a natural concept in everyday life, e.g. on an assembly line. Consider the assembly of a car: assume that certain steps in the assembly line are to install the engine, install the hood, and install the wheels (in that order, with arbitrary interstitial steps). A car on the assembly line can have only one of the three steps done at once. After the car has its engine installed, it moves on to having its hood installed, leaving the engine installation facilities available for the next car. The first car then moves on to wheel installation, the second car to hood installation, and a third car begins to have its engine installed. If engine installation takes 20 minutes, hood installation takes 5 minutes, and wheel installation takes 10 minutes, then finishing all three cars when only one car can be assembled at once would take 105 minutes. On the other hand, using the assembly line, the total time to complete all three is 75 minutes. At this point, additional cars will come off the assembly line at 20 minute increments.

Linear pipelines

A linear pipeline processor is a series of processing stages and memory access.

Non-linear pipelines

A non linear pipelining (also called dynamic pipeline) can be configured to perform various functions at different times. In a dynamic pipeline there is also feed forward or feedback connection. Non-linear pipeline also allows very long instruction word.

Q::48 The cost of a parallel processing is primarily determined by:

(A) Time complexity    

(B) Switching complexity

(C) Circuit complexity

(D) None of the above

Answer: B

Explanation:

In digital signal processing (DSP), parallel processing is a technique duplicating function units to operate different tasks (signals) simultaneously. Accordingly, we can perform the same processing for different signals on the corresponding duplicated function units. Further, due to the features of parallel processing, the parallel DSP design often contains multiple outputs, resulting in higher throughput than not parallel.

Consider a function unit (F₀) and three tasks (T₀, T₁ and T₂). The required time for the function unit F₀ to process those tasks is t₀,t₁ and t₂ respectively. Then, if we operate these three tasks in a sequential order, the required time to complete them is t₀ + t₁ + t₂.

However, if we duplicate the function unit to another two copies (F), the aggregate time is reduced to max(t₀,t₁,t₂), which is smaller than in a sequential order.

Q::49 A data warehouse is always ....................

(A) Subject oriented    (B) Object oriented

(C) Program oriented (D) Compiler oriented

Answer: A
Explanation:

In computing, a data warehouse (DW or DWH), also known as an enterprise data warehouse (EDW), is a system used for reporting and data analysis. DWs are central repositories of integrated data from one or more disparate sources. They store current and historical data and are used for creating analytical reports for knowledge workers throughout the enterprise. Examples of reports could range from annual and quarterly comparisons and trends to detailed daily sales analysis.

The data stored in the warehouse is uploaded from the operational systems (such as marketing, sales, etc., shown in the figure to the right). The data may pass through an operational data store for additional operations before it is used in the DW for reporting.

50.    The term 'hacker' was originally associated with:

(A) A computer program

(B) Virus

(C) Computer professionals who solved complex computer problems.

(D) All of the above

Answer: C